2nd Differential Solver Free 2.1 MOD APK for Android

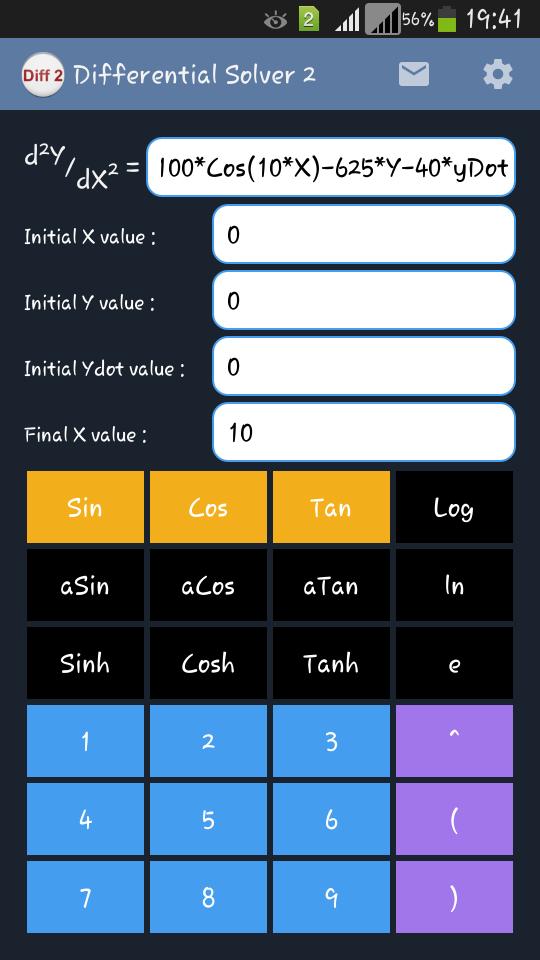
Научный инструмент для решения нелинейных обычных дифференциальных уравнений второго порядка

Научный инструмент/решатель для решения «Обычные нелинейные нелинейные обычные дифференциальные уравнения второго порядка». Приложение очень полезно для инженеров, ученых, экономистов для изучения поведения нелинейной системы, встречающейся в практических проблемах. Приложение вычисляет значение y и dy/dx при любом данном значении x (с заданными начальными значениями x, y и dy/dx). Отношения между XY и X-DY/DX могут быть визуализированы с использованием функций «сюжет y» и «ydot», соответственно. Результаты вместе с «сюжетом» можно отправить на любой идентификатор электронной почты, используя опцию «Отправить электронное письмо». Приложение имеет очень богатый и очень удобный пользовательский интерфейс (пользовательский интерфейс). Результаты могут быть отправлены на любой идентификатор электронной почты, используя опцию «Отправить электронное письмо» в главном меню.

Пожалуйста, прочитайте формат уравнения, указанный в помощи, прежде чем пытаться решить сложные нелинейные уравнения.

Оплаченную версию приложения можно найти в

https://play.google.com/store/apps/details?id=com.ashermobile.math.diffsolver2

Это приложение поддерживается рекламой.

★ Области применения: некоторые из областей применения:

• Физика и науки

• Инжиниринг

• Финансы и экономика

• промышленность

•Исследовать

★ Кто должен купить это приложение?

-Researchers

-Энджеры

-Инжинирирование студентов

-Каука студентов

★ Зачем покупать это приложение?

- Решает дифференциальное уравнение в быстрое время

- сокращает время в расчетах.

-Измеряет усилия и время в исследованиях.

★ Советы и примечания:

• Всегда рекомендуется, чтобы пользователь использовал как меньшую разницу в конечном и начальном X, чтобы получить «более высокую точность» и «лучшее разрешение на графике». Это можно сделать с помощью процесса шага, как описано ниже.

• Например, чтобы найти значение y при 10 с начальным значением x как 0, y как 0 и ydot как 0 для d2y/dx2 = cos (x)*sin (x). Чтобы получить более высокие точные результаты, разделите диапазон от 10 на 2 «шага» (от 0 до 5 и 5-10). Для первого шага введите уравнение и начальное значение x As 0, y y 0, ydot как 0 и конечное значение x как 5. Нажмите «Рассчитайте», чтобы найти значение y и ydot при x = 5 как «1,3180026397909919» и «0,4597678826781876» соответственно. Теперь для второго шага введите уравнение и начальное значение x As 5, начальное значение Y как 1,3180026397909919, начальный YDOT как 0,45976788267781876 и окончательное значение x As 10. Click «Рассчитайте», чтобы найти значение Y и YDOT при x = 10 AS «2,385818184618577414» и yDOT при x = 10 AS «2,385881844618577414» и yDOT при x = 10 AS «2,38588184461857777» и «ydot» и x = 10 AS «2,3858818184618777» и yDOT при x = 10 AS a AS «2,385818184611877» и YDOT. «0,1479794846781928».

• Когда приложение возвращает «NAN», либо значение (i) Y и DY/DX не существует в конечном диапазоне x или (ii) слишком велик, попробуйте уменьшить разницу в начальном и конечном x и используйте процесс шага, описанный выше (это особенно необходимо для функций с большой кривизны, такой как TAN и log).

• Основываясь на возможностях и ограничениях системы Android, максимальная разница в начальном и конечном x для «расчета», «сюжета» и «график ydot», которая фиксирована как «50», «30» и «30» соответственно. Для Y и DY/DX в диапазоне более 50 используйте процесс шага, описанный выше. (Для более крупного рейнджера 200 и 100 для расчета и построения построения, попробуйте платное приложение)

★ есть предложения или проблемы?

По электронной почте [email protected], и вы получите быстрый ответ.

Что нового в последней версии 2.1

★ Сделано приложение для Android 5.0

★ Исправлены незначительные ошибки.